Notes of Enrico Fermi start from an analogy between mechanics and optics and with 4 pages he derives the Schrödinger equation. In all my courses, I have seen as an axiom - this is how wave-particles behave. Here it is being derived from Fermat's least action principle.
Maupertuis Principle -- $$S = \int mv\,\mathrm ds = \int p \,\mathrm dq$$
- This is integral over phase space so this is not the same as Hamilton principle $$S = \int L \, \mathrm dt$$
- Maupertuis felt space and time should be put on equal footing
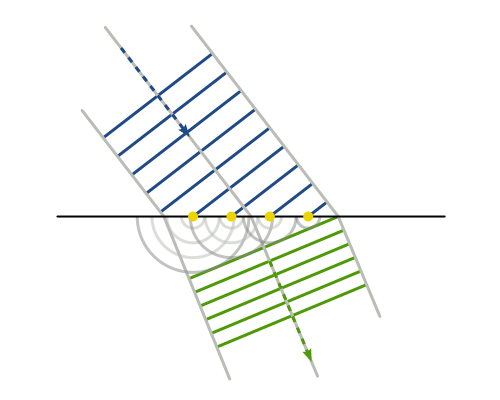
Fermat principle -- $$S = \int n \, \mathrm ds$$ principle of least time, Snell's law of refraction, etc
- this is principle of least time rather than principle of least action
- Similar to Huygens principle.
Can Quantum Mechanics be understood in terms of wave-fronts and their singularities? I would wonder what how the free particle or scattering might look in this setting.
The only other source I could find is Sir Michael Berry, who has written quite a lot.
No comments:
Post a Comment